Comparison of ASPEN Modeling System Results to Monitored Concentrations
|
Table of ContentsII. Raw Materials i) Completeness check and computation of annual
averages c) Known missing
sources i) Estimates at monitoring sites ii) Estimates at census tract centroids III. Model-to-Monitor Comparison Analysis
Methods ii) Ratio box plots iii) Percent of sites estimated "within
a factor of x" IV. Uncertainties 2) Stack parameters,
fugitive vs. stack b) Spatial and temporal
allocation in EMS-HAP V. General Results b) Location uncertainty
results
I. IntroductionOne way to evaluate a dispersion model like the Assessment System for Population Exposure Nationwide (ASPEN) is to compare its ambient concentration predictions to comparable monitoring data. As part of the National Air Toxics Assessment (NATA) initial national-scale assessment, ASPEN has predicted annual average ambient concentrations for 34 hazardous air pollutants (HAPs), 33 urban HAPs, and diesel particulate matter at approximately 60,000 census tract locations nationwide for the year 1996. In 1996 there were only several hundred air toxics monitoring sites across the US. Many of these sites, which were primarily designed and maintained under existing criteria air pollutant monitoring programs (e.g., Photochemical Assessment Monitoring Stations, or PAMS; State and Local Air Monitoring Stations, or SLAMS; Interagency Monitoring of Protected Visual Environments, or IMPROVE), only monitored a handful of HAPs for a limited period of time. Where data allow, we can compare the 1996 annual averages from these sites for the HAPs they are designed to monitor to the 1996 annual averages predicted by ASPEN for the corresponding geographic location. By comparing ASPEN predictions with the available monitoring data, we should be able to better understand the overall performance and limitations of the ASPEN model. ASPEN model predictions will then be used in the initial national-scale assessment to predict national exposure and risk values. These predicted exposure and risk levels will subsequently help the Agency in setting priorities for its air toxics programs. This document describes the results of a model-to-monitor comparison we conducted for a subset of the 33 urban HAPs. We view this comparison as a evaluation of ASPEN and the inputs that go into ASPEN, including: emissions data from various sources including the National Toxics Inventory (NTI), the Emissions Modeling System for Hazardous Air Pollutants (EMS-HAP), and meteorological data. For most of the pollutants evaluated, we found that ASPEN estimates tended to be lower than the monitor averages at the exact locations of the monitors. In general it appears that ASPEN is underestimating monitor-based HAP concentrations. Possible reasons for ASPEN to underestimate HAP concentrations include: 1) The National Toxics Inventory (NTI) missing specific emissions sources (for many of the sources in the NTI some of the emissions parameters are defaulted or missing) 2) Emission rates being underestimated in many locations. We believe the ASPEN model itself is contributing in only a minor way to the underestimation. This is mainly due to output from the antecedents of the ASPEN model comparing favorably to monitoring data in cases where the emissions and meteorology were accurately characterized and the monitors took more frequent readings. In simulations we ran, the ASPEN's estimates compared favorably to the estimates derived from a more meticulous model. 3) Monitor siting may have also contributed to the underestimation. Sites are normally situated to find peak pollutant concentrations, which implies that errors in the characterization of sources would tend to make the model underestimate the monitor values. 4) Finally, we are not sure of the accuracy of the monitor averages, which have their own sources of uncertainty. Our results suggest that the model estimates are uncertain on a local scale (i.e., at the census tract level). We believe that the model estimates are more reliably interpreted as being a value likely to be found within 30 km of the census tract location. There are many differences between the evaluation for the 1990 assessment and the 1996 assessment, including: different evaluation methods; different emissions inventories; and, different list of pollutants assessed. However, most of the model estimates in the 1990 assessment, as in the 1996 assessment, were lower than the monitor averages. Because of the variety of uncertainties involved and their importance to the model-to-monitor comparisons, we focus a good portion of the discussion in this document on assessing these uncertainties. II. Raw MaterialsA. List Of Pollutants.The EPA conducted this comparison for seven pollutants: benzene,
perchloroethylene, formaldehyde, acetaldehyde, cadmium, chromium and
lead. These pollutants were chosen because:
Benzene and perchloroethylene are volatile organic compounds (VOCs); formaldehyde and acetaldehyde are aldehydes; and cadmium, chromium, and lead are metals. The VOCs and aldehydes are gaseous, while the metals are particulate matter. B. Monitoring Data.EPA's Office of Air Quality Planning and Standards (OAQPS) currently maintains an Air Toxics Data Archive of toxics monitoring data. Much of these data are already publicly available via the Aerometric Information Retrieval System (AIRS). The data not already in AIRS have been collected from various monitoring agencies and by OAQPS over the past few years. More details on the structure and contents of the Archive are available from EPA.2 EPA hopes to make all the data in the Archive publically available within two years. i) Completeness check and computation of annual averages.To facilitate model-to-monitor comparisons, all monitoring data were converted to 1996 annual averages since all ASPEN model estimates are annual averages for 1996. Monitor data annual averages were computed using the following guidelines: 1. A measurement was considered below the method detection
limit (MDL) if either it is indicated as being below the MDL (e.g.,
value of -888 in the data archive), or if it was specified with a
numeric value that is lower than the reported MDL value for that pollutant/monitor/time
combination. If there was no reported MDL, the lowest reported
value for the pollutant/monitor combination was assumed to be the
"plausible MDL". Measurements below the actual or plausible
MDL were assigned one of three values depending on the averaging statistic
being calculated:
All annual averages used in this document are of the first type. 2. For each pollutant/monitor combination, an annual average was calculated stepwise from temporal averages of shorter durations, as indicated below. At each step the data set was assessed for completeness and retained for further processing only if the completeness criteria were met for the given averaging period. a. Daily average. A day was considered complete if the total number of hours monitored for that day is 18 or more (i.e., 75 % of 24 hours). For example, 18 hourly averages, 3 six-hour averages, or 3 eight-hour averages would satisfy the daily completeness criteria. b. Quarterly average. Calendar quarters are Winter (Jan-March), Spring (April-June), Summer (July-Sept), and Fall (Oct-Dec). A calendar quarter was considered complete if it has 75 % or more complete days out of the expected number of daily samples for that quarter, and if there were at least 5 complete days in the quarter. To determine the expected number of daily samples, the most frequently occurring sampling interval (days from one sample to the next sample) was used; in cases of ties, the minimum sampling interval was applied. c. Seasonal average. The seasons are composed of 2 quarters: Winter/Fall and Spring/Summer. A season was considered complete if it had at least 1 complete quarter. d. Annual average. An annual data set was considered complete if it had 2 complete seasons. ii) MDL.The MDL is the lowest level at which we have confidence in a monitored value. It is defined in the Code of Federal Regulations3 as the lowest value at which we can be 99% confident that the true concentration is nonzero. This value varies by pollutant and by monitor. As described in the previous section, hourly and daily monitor readings below the MDL were replaced by one-half the MDL for computation of monitor averages. For some pollutant/monitor combinations with complete data for 1996, many of the monitor readings are below the MDL. These sites are referred to as "low concentration" sites. For these low concentration sites, we do not have much confidence in the monitored annual averages, because of the uncertainty introduced when replacing values below MDL with one-half the MDL. Because of this uncertainty, only pollutant/monitor combinations with at least 50% of data above the MDL were included in the comparison. In the CEP model-to-monitor comparison,1 only pollutant/monitor combinations with at least 90% of data above the MDL were included. The cutoff percentage we chose was a compromise between ensuring high quality monitoring data and ensuring that our sample size was large enough to compute meaningful statistics. In general, we believe that monitored averages for pollutant/monitor combinations which have more than half their observations below the MDL are too uncertain to be used in a model-to-monitor comparison. iii) Flagging.We discarded pollutant/monitor combinations from the model-to-monitor
comparison if any of the following were true:
a) Dubious Accuracy. We discarded pollutant/monitor combinations for which we had reason to doubt the accuracy of the monitoring annual average. In areas with few major point sources, we would expect both toluene and benzene (both emitted primarily by mobile sources) to be highly correlated in the ambient air. Thus, if a site had an unusual ratio of toluene to benzene, we discarded the site from the site list for benzene. Levels of formaldehyde/acetaldehyde should also be highly correlated in the ambient air using the same argument as that for benzene/toulene. Thus, sites with unusual ratios of formaldehyde to acetaldehyde were eliminated from the site list for both pollutants. Sites which had extremely high monitoring values compared to other values for that pollutant were also discarded. b) Border Sites. Some of the monitoring sites are very close to the US-Mexico border or the US-Canada border. Because we are not using emissions data for Mexico or Canada, we do not have confidence in the model estimates for these sites. This is especially true of sites in Calexico, CA; El Paso, TX; Brownsville, TX; and Bellingham, WA. These sites are close to large cities on the other side of the US border. Even though we discarded these sites from the comparison, it should be noted that we are using model estimates at census tracts along the border in NATA. In preliminary runs, the model estimates were much lower than the monitor averages at these sites for all pollutants. The model estimates will almost certainly be lower for census tracts near international borders, especially when large sources are located on the other side of the border. The absence of emissions data from Mexico and Canada is a weakness of NATA. c) Known Missing Sources. In a few cases, we discovered that a source near a monitor had been missing from the initial emissions inventory. We discarded these pollutant/monitor combinations because: 1) they skewed our results (the model estimate is near zero, but the monitor average is significant) and, 2) because they do not provide a meaningful test of model performance. We will add these missing sources to the NTI in the future. However, only a small number of pollutant/monitor combinations were discarded for this reason. In order to better evaluate the performance of the modeling system as a whole, future evaluations of the ASPEN modeling system should not exclude sites along the border or sites associated with missing emissions sources. We recommend including these sites in the analyses and explaining any disagreement between model estimates and monitor averages, instead of discarding them. C. Emissions Inventory.The ASPEN model uses emissions and meteorology data as inputs. The "raw" emissions inventory data is primarily from the National Toxics Inventory (NTI). The NTI data are made "model-ready" by the Emissions Modeling System for Hazardous Air Pollutants (EMS-HAP). A user's guide on EMS-HAP will be available soon. i) NTI.The NTI contains extensive air toxics emission estimates for four source types: major, area and other, onroad mobile, and nonroad mobile. Some of these sources are point sources with specific geographic coordinates. These fall into the "major" or "area or other" category, depending on the amount of emissions. The remaining non-point sources are summarized at the county level. More extensive information about the NTI is available elsewhere on the NATA web site. The NTI is a very important input to the ASPEN model. Estimates from ASPEN are highly sensitive to emission rates, locations, and release parameters (such as height and velocity) in the vicinity of sources. Much of our study of the uncertainties of the model estimates in this paper focus on the NTI.. ii) EMS-HAP.For mobile and area sources, NTI estimates are at the county level. All NTI emissions represent total annual emissions. The ASPEN model, however, requires higher resolution both temporally and spatially. EMS-HAP allocates the emissions from the NTI temporally and spatially, for use in the ASPEN model. Temporally, EMS-HAP allocates the annual total emissions into eight three-hour periods within an annually averaged day. Each day of the year is allocated the same emissions. EMS-HAP spatially allocates non-point, county-level emissions to the census tracts within each county, as required by the ASPEN model. EMS-HAP allocates these emissions based on surrogates such as population, land use, roadway miles, etc., depending on the source category. For point source emissions, spatial allocation is not performed because most point sources in the NTI already have exact latitude/longitude coordinates. When point source geographic coordinates are missing, EMS-HAP uses default values wherever possible. For example, if the geographic coordinates for a point source are missing but the zip code is not, EMS-HAP assigns the lat/lon coordinates of the zip code's centroid to the source. If the zip code is missing but the county is not, EMS-HAP assigns to the source the lat/lon coordinates of a census tract centroid chosen randomly from the county. We will discuss some of EMS-HAP's allocation and default techniques in the uncertainties section of this document. D. Model Results.Two types of ASPEN model estimates are used in this comparison: 1) estimates at the exact location of the monitors, and 2) estimates at every census tract centroid in the U.S. The first type of estimate was generated specially for the purpose of doing a model-to-monitor comparison. The second type of estimate is an integral part of NATA; these estimates are fed into the exposure and risk assessments. Procedures to run ASPEN for either type of estimate are identical. i) Estimates at monitoring sites.We used the ASPEN model to estimate concentrations at the exact locations of the monitors, to get point-to-point comparisons. Most of the analyses in this document use the results of this point-to-point comparison. ii) Estimates at census tract centroids.All other model results on the NATA web page use the tract-level model estimates. We use the tract-level estimates in this comparison for the MAXTOMON test described in section III.B.iv. III. Model-to-Monitor Comparison Analysis MethodsWe describe some of the analytical tools used in this report below. All but one of these tools deal with point-to-point comparisons in that they examine whether the model's estimates agree with monitor average readings at the exact monitor location. The one tool that does not use only a point-to-point comparison is the MAXTOMON tool, which compares the monitor average to the maximum of model estimates within a circle around the monitor. This type of test allows for more uncertainty in parameters such as: locations of sources and monitors, release heights, meteorology, etc. A. Graphical.i) Scatter plots.Scatter plots are a relatively straightforward graphical way to show the relationship between two variables. We simply plot model estimates of annual averages against monitor averages. Each ordered pair on the graph is (model, monitor), for each monitoring site for that pollutant. For example, if we have 90 monitors for benzene, we will have 90 ordered pairs to plot. We will also show the 2:1, 1:1, and 1:2 lines on the plots. We consider the model estimates to be "good" for a pollutant/monitor combination if the point falls between the 2:1 and 1:2 lines. In modeling terminology, we call this "agreement within a factor of 2". The model is performing well for a given pollutant if most of the points fall between the 2:1 and 1:2 lines. ii) Ratio box plots.Ratio box plots show the same data as the scatter plots but in a
different fashion. Each box shows the distribution of model-to-monitor
ratios. For example, if we have 50 monitors for perchloroethylene,
we will have 50 model/monitor ratios to compute. We then compute
the mean of these 50 ratios as well as the percentiles to then create
a box plot. The plots will show the median, 25th, and 75th percentiles of the
ratios. If the model is performing well, the box plots will
be short, and centered at around 1. We decided not to show more extreme percentiles (e.g., 10th and 90th) of the ratios because often the extreme percentiles were far from the center of the distribution. In our study, sometimes model estimates of near zero are paired with significant monitor averages, due to missing sources or sources with defaulted or incorrect locations. These result in ratios near zero, which skew the distribution of the ratios. Less often, we'll see high model estimates paired with low monitor averages. But because ratios take extreme values so often, we decided to only show the interquartile range of the distribution. There is an additional reason for leaving out the extreme percentiles. Given values with large uncertainty, high percentiles tend to be biased high and low values tend to be biased low.4 This is because the values with large positive errors will collect in the high end of the distribution, and values with large negative errors will collect in the low end of the distribution. We decided to use a logarithmic scale for the vertical axis for the following reason. If we use a regular arithmetic scale on the vertical axis, then a ratio of 2 is twice as far from 1 as a ratio of 1/2. However, modelers typically speak of estimates as "within a factor of x." An underestimate by a factor of x should look just as erroneous as an overestimate by a factor of x. A logarithmic scale makes the overestimation and underestimation the same distance from the horizontal line where the ratio is 1. The ratio box plots in this document will be shown side-by-side, one for each pollutant. This will allow us to see easily which HAPs are being overestimated and underestimated, and which are being estimated consistently. B. Statistical.i) Number of sites.The number of sites is the number of monitors for each pollutant which were not filtered out by any of the criteria in section II.B. A larger number of monitors means more data is available which in turn would lend more accuracy to the comparisons. Lead and benzene have the highest number of monitors. ii) Median of ratios.The median of ratios is based on the model/monitor ratios for a given pollutant. A median close to 1 suggests that the model overestimates the monitors about as often as it underestimates the monitors. This statistic is also shown on the ratio box plots. iii) Percent of sites estimated "within a factor of x".This statistic is also based on the model/monitor ratios for a given pollutant. We will often look at the percent of sites for a given pollutant which agree within a factor of 2, which is the percent of sites for which the model estimate is somewhere between half and double the monitor average. We'll also talk about the percent of sites estimated within 30%: this is the percent of sites for which the model/monitor ratio is between 0.7 and 1.3. iv) MAXTOMON.This technique compares the MAXimum model estimate within r kilometers of the monitor TO the MONitor average. All model estimates are considered (both estimates at monitor sites as well as the estimates at census tract centroids) in finding the maximum values. This is an example of a point-to-range tool. We use this tool to test whether the frequent underestimation by the model at monitoring sites was due to location uncertainties or due to systematic underestimation. To explain further, let's say the model estimate for a certain pollutant/monitor combination was much lower than the monitor average. We might wonder if the model predicted a concentration similar to the monitor average anywhere near the monitor site. If it did, it is possible that the underestimation at the exact monitor site was due to uncertainties in the inputs to the model (especially in source locations), instead of due to systematic underestimation by the model. In general, we hope to see very few monitor averages underestimated by the model as r gets large. One weakness of the MAXTOMON test is that there is a sparser network of model receptors in rural areas than in urban areas, because the census tracts are larger. Thus, the MAXTOMON test might have more difficulty finding a peak concentration in a rural area than an urban area. IV. UncertaintiesIn this section, we will look at some of the sources of uncertainties which factor into the comparison. We will begin with a historical overview of model-to-monitor comparisons done with ASPEN, to get an idea how ASPEN results compare to monitored concentrations when the comparison is done on a smaller scale, and to provide a historical context for our own comparison. In these studies, the emissions, meteorological, and monitoring data are more likely to be of higher quality than ours. We will then assess some of the uncertainties involved with the emissions and monitoring data, as well as some of the uncertainties introduced by the ASPEN itself. A. History Of Model-to-Monitor Comparisons With ASPEN.In the early years of air dispersion modeling, hand calculations were the norm as high-speed computers were not yet available. Early computers also had limited memory capabilities. This spawned the development of a particular type of dispersion model which employed a statistical summary of meteorological conditions, which then required a special algorithm for characterizing the resulting dispersion. Early examples of this type of model were described by Meade and Pasquill5, and Lucas.6 The idea was relatively simple, but most of the algorithms for characterizing the basic processes (e.g., buoyant plume rise, plume dispersion, depletion, etc.) were simplistic with little experimental verification. Basically, a computation was made for each expected wind speed and stability condition whose probability of occurrence was computed for wind sectors surrounding the source. The average concentration was then computed by summing, for each wind sector, the computed concentration at each downwind distance, multiplied by the frequency of occurrence of each wind speed and stability combination. Pooler7 described one of the first attempts to employ numerical methods for automating the computations (using an IBM 650 computer) to provide estimates of monthly average concentration values for comparison with observations of sulphur dioxide (SO2) collected daily from November 1958 through March 1959 at 123 sampling sites in Nashville, TN. We have to temper Pooler's evaluation results as regressions were performed with the observed concentration values. This was done to provide best estimates for the variation of the monthly emission rates from the known sources. When we digitized Pooler's data for reanalysis we only found 122 data values, not 123. That said, the model overestimated the observed values by a factor of 1.37 with a correlation coefficient (r2) of 0.95. (Note: In all descriptions of past model-to-monitor comparisons in this section, the reported factor of over or under estimation and correlation coefficient (r2) were deduced through a linear regression with the intercept forced to be at the origin.) We found 110 of the 122 values within a factor of 2 of the observed values, with 74 of the 122 values within 30%. Martin8 summarized the dispersion model used to numerically compute (using an IBM 1130) winter season estimates of the average SO2 concentration values for comparisons with observations collected daily from December 1964 through February 1965 at 40 sites in the St. Louis area. Removing comparison results for the five most suspect locations reduced the overestimation to 1.47 and increased the correlation coefficient to 0.95. Thirty-four of the 35 values were within a factor of 2, with 14 within 30%. A reanalysis of these same data was performed by Calder9 using the Climatological Dispersion (CDM) model, using a revised characterization of the area source emissions by Turner and Edmisten.10 A major enhancement within the CDM over the model employed by Martin was to incorporate an improved treatment for characterizing dispersion from area sources, employing an algorithm based on the narrow plume hypothesis. In spite of the attempts to improve the characterization of area source emissions and the dispersion from these low-level sources, the comparison results were similar to those achieved by Martin. The CDM tended to overpredict concentration values by a factor 1.54 with a correlation coefficient (r2) equal to 0.92. Thirty-five of 39 estimates where within a factor of 2, with 17 within 30%. Possible factors contributing to the tendency to overestimate the observed concentration values were: an inherently crude emissions inventory, no day versus night variation in emission rates, and use of inaccurate estimates of mixing heights. Turner et al.11 summarized the results obtained in applying the CDM model to estimate annual average particulate and SO2 concentration values for the New York area for 1969. SO2 observations were available for comparison at 75 locations and total suspended particulate matter observations were available for comparison at 113 locations. This version of the CDM employed the Briggs12 plume rise algorithms (in contrast to use of Holland13 algorithms used by Martin and Calder in the St. Louis comparisons). For SO2 it appears the CDM tended to slightly overpredict concentration values by a factor of 1.11 with a correlation coefficient (r2) equal to 0.90. Seventy-one of the 75 values were within a factor of 2, with 47 values within 30%. For particulates it appears the CDM tended to slightly underpredict concentration values by a factor of 0.93 with a correlation coefficient (r2) equal to 0.94. 111 of the 113 values were within a factor of 2, with 94 within 30%. Irwin and Brown14 summarized the results obtained in applying the CDM model to estimate 1976 annual average SO2 concentration values for the St. Louis area. There were 13 sites, but omission of a lead smelter near one site precluded use of data at two sites for model performance comparisons. The emission inventory and monitoring results were obtained as part of the St. Louis Regional Air Pollution Study. These simulations differ with those computed by Turner et al. in that urban dispersion parameters (based on tracer studies conducted in St. Louis, McElroy and Pooler15 and Gifford.16 It was determined that although the area source emissions constituted only 3.5% of the total area and point source emissions, estimated concentrations from area sources ranged from 14 to 67% of the total concentration estimated at the monitoring sites. For the 11 sites it was found that CDM slightly overpredicted concentration values by a factor of 1.10 with a correlation coefficient (r2) equal to 0.96. Nine of the 11 sites have estimates within a factor of 2, with 3 values within 30% of those observed. This same inventory was simulated using the RAM model,17 which employed hourly specification of the meteorology and the emissions. For the 11 sites it was found that RAM slightly overpredicted concentration values by a factor of 1.10 with a correlation coefficient (r2) 0.96. For the RAM estimates, all 11 sites had estimates within a factor of 2, with 10 values within 30% of those observed. The version of CDM applied by Irwin and Brown is similar to the Industrial Source Complex (ISCLT) Long-Term model.18 The major difference in ISCLT is that its area source algorithm is better than that employed by CDM. ISCLT's area source dispersion characterization nearly approximates what is obtained when one computes area source impacts using an hour-by-hour simulation (which employs a double integral over the area and hence is our best expression of dispersion from an area). The emphasis on improving the treatment of area source impacts reflects the recognition that area source emissions (if present) often account for a major portion of the simulated impacts, as discussed in the previous paragraph. In the studies summarized in the table below, it is important to remember that the long-term models have evolved with the adoption of improved characterizations for the dispersion, and for treatment of area sources. Except for the simulations for Nashville by Pooler and for St. Louis by Martin and Calder, the average bias has been slight. The CDM versus RAM comparisons offer an interesting clue that perhaps the time variation of the emission rates (which Calder was the first to offer as a major concern) is of importance, although there are other differences between CDM and RAM that also might offer explanation of the differences seen. Regardless of the model employed, its estimates are generally within a factor of 2 of those observed.
|
| Table 1. Summary of long-term model simulation comparisons. Note the tendency for over or underprediction. The correlation coefficient (r2) is based on a linear regression with the intercept specified as the origin. | |||||
| Study | Number of Values |
Over/Under Factor |
Correlation (r2) |
Within Factor of 2 |
Within 30% |
| Pooler (1961) Nashville SO2 | 123 | 1.37 | 0.92 | 90% | 61% |
| Martin (1971) St. Louis SO2 | 35 | 1.47 | 0.94 | 97% | 40% |
| Calder (1971) St. Louis SO2 CDM |
39 | 1.54 | 0.92 | 90% | 44% |
| Turner et al. (1971) New York SO2 CDM |
75 | 1.11 | 0.90 | 95% | 49% |
| Turner et al. (1971) New York Particulates CDM |
113 | 0.93 | 0.94 | 98% | 83% |
| Irwin and Brown (1984) St. Louis SO2 CDM |
11 | 1.10 | 0.96 | 82% | 27% |
| Turner and Irwin (1983) St. Louis SO2 RAM19 |
11 | 1.10 | 0.96 | 100% | 91% |
| Table 2. Geographic coverage of monitoring data, by pollutant. | ||
| Pollutant | Number of Sites | Number of States |
| Benzene | 87 | 16 |
| Perchloroethylene | 44 | 8 |
| Formaldehyde | 32 | 10 |
| Acetaldehyde | 32 | 10 |
| Lead | 242 | 28 |
| Cadmium | 20 | 7 |
| Chromium | 36 | 6 |
| Table 3. Percent of daily values above MDL, by pollutant. Many of the monitors have a large percentage of data below MDL, especially for chromium. | |||||
| Number of Sites With Percent of Daily Values Above MDL | |||||
| Pollutant | Number of Monitors | 50% to <60% | 60% to <70% | 70% to <80% | >=80% |
| Benzene | 87 | 8 | 2 | 4 | 73 |
| Perchloroethylene | 44 | 2 | 0 | 1 | 41 |
| Formaldehyde | 32 | 0 | 0 | 0 | 32 |
| Acetaldehyde | 32 | 0 | 1 | 0 | 31 |
| Lead | 242 | 12 | 8 | 11 | 211 |
| Cadmium | 20 | 1 | 1 | 1 | 17 |
| Chromium | 36 | 13 | 3 | 4 | 16 |
| All | 493 | 36 | 15 | 21 | 421 |
| Table 5. Uncertainty in point source location data for metals, by state. Those States with an asterisk by their entries were less forthcoming in submitting their point source inventories to EPA. State/metal combinations are denoted by O, X, XX, or XXX, depending on the percent of point source emissions by mass which have either defaulted locations or locations falling outside the reported county. Each state/metal combination also has a pie chart associated with it, showing the breakdown of point source emissions into the location categories. | |||
| State | Lead | Cadmium | Chromium |
| Alabama* | XXX | XXX | X |
| Arizona | XX | O | O |
| Arkansas | X | O | O |
| California | O | XX | X |
| Colorado | O | O | O |
| Connecticut* | XX | X | X |
| Delaware | O | O | O |
| District of Columbia | O | O | O |
| Florida | O | XXX | O |
| Georgia* | XXX | XXX | O |
| Idaho | O | XXX | XXX |
| Illinois | O | O | O |
| Indiana | XXX | XX | XXX |
| Iowa* | O | O | O |
| Kansas | O | O | O |
| Kentucky | X | O | O |
| Louisiana | XX | O | X |
| Maine | O | O | O |
| Maryland | X | O | O |
| Massachusetts* | O | O | O |
| Michigan* | X | X | X |
| Minnesota | XX | XXX | X |
| Mississippi | XX | XXX | XX |
| Missouri | O | XX | X |
| Montana* | X | O | O |
| Nebraska | O | O | O |
| Nevada* | O | O | O |
| New Hampshire | O | O | O |
| New Jersey* | O | O | O |
| New Mexico | O | O | O |
| New York | X | XX | O |
| North Carolina | O | O | O |
| North Dakota | O | O | O |
| Ohio* | XX | XX | O |
| Oklahoma* | XX | XX | O |
| Oregon | XXX | XXX | X |
| Pennsylvania | X | XXX | O |
| Puerto Rico | XXX | XXX | XXX |
| Rhode Island | XXX | XXX | XXX |
| South Carolina | XX | X | X |
| South Dakota | O | O | O |
| Tennessee | X | XX | X |
| Texas | XX | XXX | O |
| Utah | O | O | O |
| Vermont | X | X | X |
| Virginia | XX | XXX | X |
| Washington | XX | XX | X |
| West Virginia | O | O | O |
| Wisconsin | O | O | O |
| Wyoming | O | O | O |
|
All states are placed into three categories based on their level of participation in submitting a point source inventory to the NTI: high, medium, and low. States which fall into the later two categories have been identified with an asterisk in Table 5. A state/pollutant combination is assigned an 'O' if less than 10% of its emissions are "location uncertain" (either from a source with a defaulted location or from a source falling more than 5 km outside a county boundary); an 'X' if between 10% and 25% of sources are location uncertain; an 'XX' if between 25% and 50% of sources are location uncertain; and an 'XXX' if more than 50% are uncertain. The more the location uncertainty, the less trust we have in model results for the given state/pollutant combination on a local scale. The pie charts show the percent of emissions which fall into each of the four location categories: county default; zip code default; not defaulted but more than 5 km outside the reported county; and not defaulted and either inside the reported county or less than 5 km from its boundary. All categories but the last are considered "uncertain". The more minimal the emissions which fall into the first three categories, the more we can trust the model results on the local scale (the likelihood of missing sources should also be considered). Table 6 shows the percent of emissions falling into each location
category, when summing across states. The NTI has exact geographic
locations for most of the point source chromium emissions, most
of which fall in the reported county; but about 13 percent of lead
emissions and 25 percent of cadmium emissions are default values.
In section V, we'll discuss some of the Lead results in more detail. . 2) Stack parameters, fugitive vs. stack. Other stack parameters are as equally important to model results as the location. Slight changes in the stack parameters can cause widely varying model results. We'll focus mainly on release heights. Most of our monitors measure the concentration of a pollutant on the ground, as does ASPEN. EPA modelers agree that the release height is important, because emissions released from high stacks have more air to pass through on their way to the ground than emissions released at ground-level. As a result, we might expect positive errors in release height to lead to model underestimates, and vice versa. Studies have shown that ground-level concentrations are 5 to 8 times more affected by low level emissions than by elevated emissions.20,21 In part to check the accuracy of the stack release heights in the NTI, EPA investigated a lead smelter in Herculaneum, Missouri. According to the TRI, 89.91 tons of lead were emitted from the 550-foot stack in the center of the facility, and 7.66 tons were "fugitive" emissions (that is, escaping from the facility through open doors, windows, etc). However, the emissions for an ongoing 2-month study at the facility suggest that the "fugitive" emissions are of order 50 tons rather than 7.66 tons. We can not generalize to all other sources from one site visit, but this does reveal the types of emission characterization uncertainties that can occur. All other factors being equal, an increase from 7.66 to 50 tons in low-level emissions would likely increase the predicted annual average for this site by a factor of 3. b) Spatial and temporal allocation in EMS-HAP. One of the tasks of EMS-HAP is to allocate NTI emissions summarized at the county level both temporally and spatially. EMS-HAP makes numerous assumptions in these allocation processes, which add to the uncertainty of the model estimates. The EMS-HAP user's guide will soon be available to the public. This guide will describe these allocation techniques in detail. For our purposes, it is important to note that pollutants for which area sources contribute significantly to model estimates have more uncertain model estimates. iii) Model uncertainties.A dispersion model in general makes many simplified assumptions as to the fate and transport of an emission plume. One of the key simplifications of the ASPEN model is that it does not include a terrain component in its prediction algorithms. Further, the model relies on steady-state, long-term sector-averaged climate summary data to represent the conditions at any given plume site. The model also simplifies some complex atmospheric chemical processes and captures pollution transport within only 50 km of any individual source. Dispersion Calculations ASPEN Calculations Test Case Meteorology
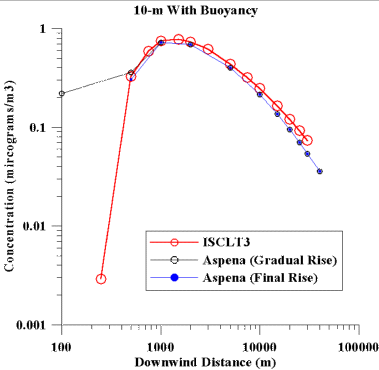
a) Interpolation. We specifically investigated whether the interpolation scheme used within ASPEN might be underestimating the actual modeled impacts. This concern arose because a "net" of receptors is employed by ASPEN, and then concentrations at specific points are estimated by interpolating within the "net". We wondered whether ASPEN might underestimate peak ambient concentrations because it "averages out" the peak values by combining them with lower concentrations nearby. To do this, we simulated three different types of emissions sources, and compared the ASPEN estimates downwind from each source to the estimates derived from a more recent, detailed version of ASPEN, the Industrial Source Complex Long-Term Model Version 3 (ISCLT3). The simulations were run under a variety of wind speed conditions. The first simulated source was a point source with a 10-m stack height. The stack gas temperature was set to be nearly the same as the ambient temperature, and the exit velocity was set at 1 m/s. In this case, there would be no plume rise. Figure 1 depicts the results obtained from the two models. It is evident that at 250 m downwind, ISCLT provides a concentration that is greater than what ASPEN would provide using its log-log interpolation procedures. However, at most distances the two models provide similar results. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
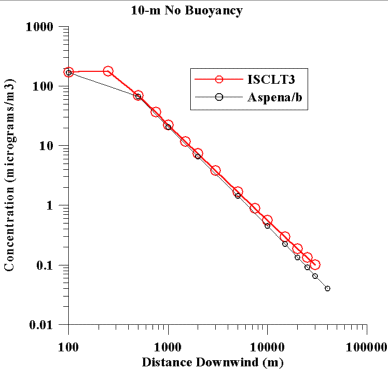 |
| Figure 1. Comparison of concentration estimated by ASPEN and ISCLT3 for a 10-m point source, with no plume rise. The emission rate was 1 g/s. |
|
The second simulated source is again a point source with a 10 m
stack height. In this case the plume was made buoyant, with
an exit velocity of 2 m/s and an exit temperature of 495 K.
The actual plume rise (Dh) is dependent
on the wind speed (u), as Dh=357/u,
where Dh is in meters and u is in m/s.
Figure 2 shows the concentrations obtained from the two models for
this buoyant source. Notice that when ASPEN is run in its
normal mode, where gradual rise is used at all distances, the ASPEN
concentration at 100 m downwind is much larger than what ISCLT estimates.
Whereas if we run ASPEN using the final plume rise at all distances
(which is how ISCLT runs), the estimates are more in line with what
ISCLT provides. The ASPEN estimates are lower than ISCLT's
by about 10% in the near distances, with the underestimation increasing
to about 25% at 30 km downwind.
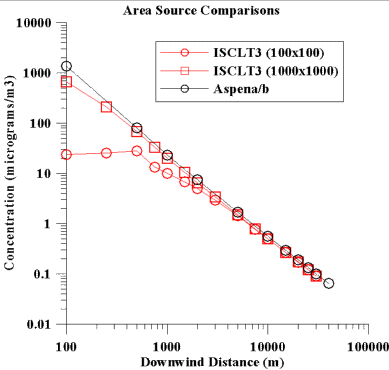
As a third case, two area sources of different size were simulated
within ISCLT for comparison with those estimated by ASPEN.
ASPEN does not explicitly assign a size to area sources, so we tried
to deal with the two different source sizes by varying the area
of the census tract. In these comparisons, the emission rates
were 1 g/s from each area source (which is expressed as g/s-m2 in
ISCLT). Figure 3 depicts the comparison results obtained.
As seen in Figure 3, once one is 3 km or more downwind, the differences
are less than 20%.
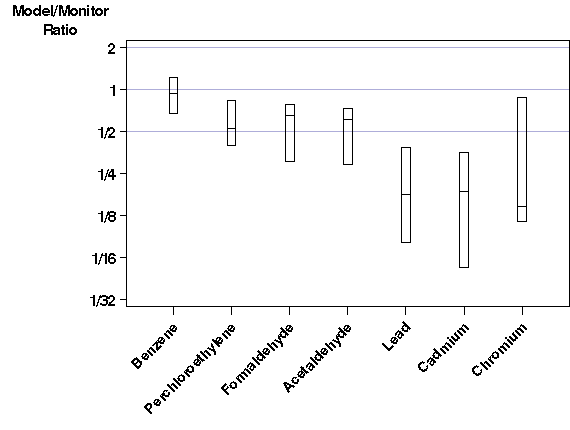
In these comparisons, we see no systematic bias in the ASPEN calculations that would cause it to significantly underestimate concentration values in comparison to ISCLT. If anything, it appears that ASPEN may provide higher concentration values for receptors near or within tracts with area source emissions. b) Deposition. When calculating ambient concentrations, ASPEN simulates the effect of dry deposition of particulate by adding an additional decay term to the emission rate. The decay term is a function of the deposition velocity, downwind distance from the source, and plume dimensions (with respect to the mixing height). Deposition velocity is also a function of the particle size, wind speed, and the land-use type. The ASPEN model allows different deposition options for fine and coarse particulate and urban/rural environments. In order to analyze the effect of these options on the modeled ambient concentrations, we performed test case simulations using lead emissions from mobile non-road sources in Colorado. We used different compositions of fine/coarse fractions and held the total emission rate constant. Five different scenarios were used for this test case: 10% fine and 90% coarse, 25% fine and 75% coarse, 50% fine and 50% coarse, 75% fine and 25% coarse, and 90% fine and 10% coarse. Emissions from 17 pseudo-point sources of 10 m height, 1 m/s exit velocity, and T = 295 K were considered. For fine particles, the deposition velocities are generally similar and scattered around the 1:1 ratio line. The deposition velocities for coarse particles are much higher for ASPEN than for ISCST3. The effects of these differences was extrapolated to the national scale. For the entire U.S., the total lead emissions were 66.5 g/s and the percent contribution from different source categories was as following: 49% all lead emission were accounted for by major sources, 28% by area sources, less than 0.01% by mobile on-road, and 23% by mobile non-road sources. For the ASPEN simulations this means that about 50% of all lead emission sources were treated as point sources and about 50% as pseudo point sources. We estimated that ASPEN has a bias to predict average lead concentrations in the air 20-30% lower than one would typically predict, because it employs coarse particle deposition velocities that are higher than one would usually use. The same logic applies to the other particulate HAPs in the comparison (cadmium and chromium). We expect that the percent of emissions in the coarse category for these other two is less than that for lead, however, so we would expect the underestimation bias also to be less. V. General ResultsA. Overall.The ratio box plot below gives a general idea of the results of the point-to-point comparison.
For comparison to the results from historical literature (see section IV.A), the table below gives the percentage of sites estimated within 30% and within a factor of 2. It also reports the percentage of sites which are underestimated by the modeling system.
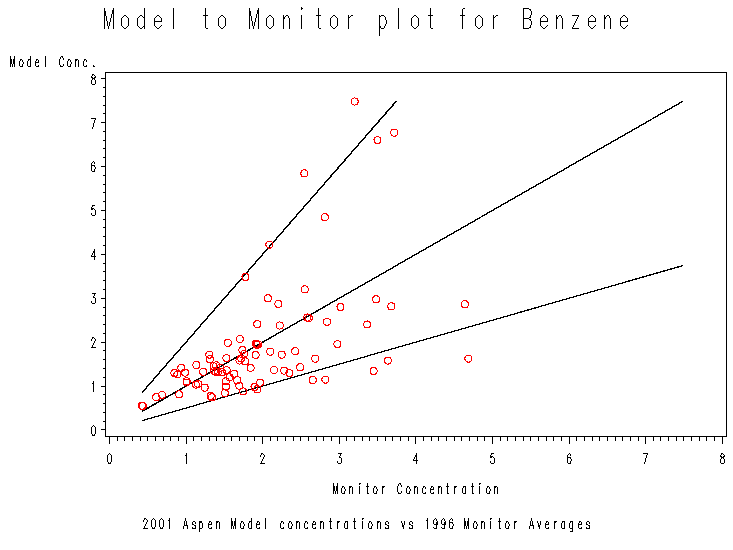
These results are surprising given the results of the historical studies. Only for benzene is there comparable agreement between our results and historical studies on a point-to-point basis. The remainder of the pollutants show poor agreement on a point-to-point basis, with the model estimates systematically lower than the monitor averages. From the ratio box plot graph, we can see that this is especially true for the three metals, which all have ratio medians of less than 1/5. This means that on average they are underestimated by more than a factor of 5. This is most interesting for lead, because this is a well-studied criteria pollutant, for which we have extensive monitoring data as well as a detailed emissions inventory. Because past model-to-monitor studies (see section IV.A) show much better agreement than this particular study, something must be different in this study compared to previous studies comparing model results to monitor data . We do not feel that the underestimation is due to the model itself, because the model employed here is very similar to the model used in all the historical studies. Possible explanations for the systematic underestimation in this work include: 1. The emission rates are systematically underestimated and/or many sources are missing from the emissions inventory. 2. Many of the monitors were likely sited to find peak concentrations. Often, the ambient concentration falls off quickly around the peak area. Even under the scenario of a "perfect" model and "perfect" monitors, if the monitor is situated right at the peak and the emissions or meteorological inputs are even slightly inaccurate, the model will tend to underestimate results. This is especially likely for pollutants dominated by point sources with elevated releases, because any errors in release height, exit velocity, and/or emissions location will likely cause the model to find a peak concentration area different from the true peak. The MAXTOMON statistic described in section III.B.iv is especially designed to investigate the second explanation on why there seems to be a systematic underestimation by the model in this work. B. Benzene.The ratio box plot (Figure 4) and short list of statistics (Table 8) in the previous section show good agreement between model output and monitor data for benzene. Below is the scatter plot. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Figure 5. Model-to-monitor scatter plot for benzene. Most points fall within the factor of two wedge, and none are far outside the wedge. |
|
As expected from Figure 4 and Table 8, most of the points in the scatter plot fall between the 2:1 and 1:2 lines. The high- concentration monitors seem to be estimated less reliably. Most of the points falling outside the "factor of 2 wedge" are those with high monitor concentrations. "Misses" are both low and high, but note that none of the points "miss" by a large margin. The largest model-to-monitor ratio is 2.45 and the smallest is 0.34, so all monitors are estimated within a factor of three. There are several reasons why we would expect good agreement between
model prediction and monitor results for benzene:
C. Other Gases.In the ratio box plot in section V.A., we can see that agreement is similar for the three other gases in the study: perchloroethylene, formaldehyde, and acetaldehyde. The model's estimates tend to be lower than the monitor averages, but the ratio medians are all within a factor of 2. Perchloroethylene is dominated by area sources. For the average census tract across the US, area sources are responsible for 49% of the perchloroethylene model estimate. Modeled concentrations of both aldehydes are dominated by onroad and nonroad mobile sources, the percent contribution of mobile sources is 69% for formaldehyde and 90% for acetaldehyde. For area and mobile sources, we rely heavily on the spatial allocation methods of EMS-HAP, which add uncertainty to the model estimates. Because of the uncertainty involved in the spatial allocation methods, it is possible that the model is estimating a concentration at or higher than the monitor average nearby, but not at the actual monitor location. Thus, let's look at the MAXTOMON results for all three gases. Benzene is also included for comparison purposes. |
| Table 9. MAXTOMON table for the four gases. The two VOCs have high modeled concentrations near the monitors most of the time, even if they are underestimated at the exact monitor locations. This is also true for the two aldehydes, but to a lesser degree. | |||||||||
| Percent Missing Low at Radius Of: | |||||||||
| Pollutant | # Monitors | 0 km (Exact Monitor Location) |
2 km | 4 km | 6 km | 8 km | 10 km | 20 km | 30 km |
| Perchloroethylene | 44 | 86% | 73% | 61% | 59% | 52% | 43% | 23% | 9% |
| Formaldehyde | 32 | 88% | 81% | 78% | 69% | 59% | 56% | 31% | 31% |
| Acetaldehyde | 32 | 91% | 91% | 84% | 69% | 56% | 56% | 38% | 34% |
| Benzene | 87 | 59% | 47% | 36% | 30% | 26% | 25% | 20% | 11% |
|
The percent of monitors underestimated drops off quickly for perchloroethylene. The model's estimate is low on a point-to-point basis 86% of the time; but there are modeled concentrations nearby which are greater than or equal to the monitor average for many of the monitors. Less than half the sites are underestimated if we go out 10 km; and less than a quarter are underestimated if we go out 20 km. This suggests that uncertainties in the location of the nearby area sources may be responsible for the underestimation on a point-to-point basis. The effect is less dramatic for the two aldehydes, but still evident. If we go out 20 km, 31% of the formaldehyde and 38% of the acetaldehyde monitors are underestimated, compared with 88% and 91% at the actual monitor locations. The aldehydes differ from the five other HAPs examined in this comparison because a significant portion of their ambient concentrations are formed through a secondary process in the atmosphere. The other HAPs are relatively inert, which makes them easier to model. ASPEN simulates atmospheric chemical reactions for the aldehydes in a very simplistic manner which makes it an additional source of uncertainty. It is very possible that the ASPEN model underestimates the amount of secondarily-formed aldehydes. Analysis of ASPEN modeled nationwide mean values for formaldehyde and acetaldehyde suggest that 23% and 58% (respectively) of the total modeled concentrations are attributable to secondary formation. A more recent study using OZIPR (a photochemical grid model) suggests that secondary formation generally accounted for approximately 90% of the ambient formaldehyde and acetaldehyde.22 These results loosely suggest, especially for perchloroethylene, that the model is not necessarily systematically underestimating ambient concentrations, it may just be finding the peak concentration in the wrong place. D. Metals.As discussed previously, the underestimation at the actual monitoring locations is severe for the three metals, all of which have ratio medians of less than 1/5. i) Lead.Monitored concentrations of lead in the US today tend to be high only near lead point sources. Of the 242 lead monitors in the study, 106 (44%) are designated as source-oriented. Both the source-oriented monitors and the other monitors are underestimated by the modeling system at the monitor locations. Typically (using the median), the source-oriented monitors are underestimated by a factor of 7.5, and the others are underestimated by a factor of 4.9. Only 17% of the source-oriented monitors and 18% of the other monitors are estimated within a factor of 2. Since the underestimation at the source-oriented monitoring sites is the most severe, we investigated more closely the model estimates at some of these monitor sites. We did not look at all 106 monitors which were labeled as source-oriented in the Archive, however. The decision to define a monitor as source-oriented is somewhat subjective. A monitor placed well downwind of a source in a residential neighborhood might be considered source-oriented by some but population-oriented by others. Because of this, we chose to look closely at a subset of the monitors which best fit the mold and definition of a source-oriented monitor (further subsetting by monitored concentration). Previous experience suggests that a monitor with an annual average of 0.3 mg/m3 or higher is certain to be source-oriented. Of the 242 monitors used in the comparison, 42 are both labeled as source-oriented and have monitored annual averages greater than 0.3 mg/m3. The median underestimation factor for these 42 monitors is 16.7. We have two possible explanations for these large underestimations:
The uncertainties involved in the deposition algorithm of the ASPEN model (section IV.B.iii.b) and the uncertainties involved in the estimation of fugitive emissions (section IV.B.ii.a.2) also are likely contributors to underestimation. We could think of no convenient way to test the first hypothesis. We can test the second hypothesis by: 1) using MAXTOMON methods and by, 2) looking at the percent of defaulted emissions near the source. We did both. In order to focus more closely on what caused the underestimation, we looked only at the 30 of the 42 monitors which were underestimated by a factor of 10 or greater. For the sake of brevity, we will call these the "discordant monitors". a) MAXTOMON results. The model receptors used in the MAXTOMON tests included exact monitor locations and tract estimates. But since many of the lead sources are in rural areas, away from urban areas and their small census tracts, the network of receptors used in the MAXTOMON test is not that dense. Thus, it is possible that the model could be simulating a peak concentration near the monitor, but none of the tract centroids or monitor locations are near this peak. For this reason, we feel that the MAXTOMON test is not as effective (without adjustment for receptor network size) in areas of low population density. Here are the MAXTOMON test results: |
| Table 10. MAXTOMON table for the discordant lead monitors. 29 of the 30 discordant monitors have no higher modeled concentrations within 30 km. | ||||||||
| Percent Missing Low at Radius Of: | ||||||||
| # Discordant Monitors | 0 km (Exact Monitor Location) |
2 km | 4 km | 6 km | 8 km | 10 km | 20 km | 30 km |
| 30 | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 97% |
|
So even a search radius of 30 km brings only one discordant monitor out of "underestimated" status. b) Location uncertainty results.
The following table shows the percent of emissions falling into
each of the four location categories for each of the discordant
monitors. Included are all sources with reported locations
within 50 km of the monitor. |
| Table 11. The 30 discordant monitors and location categories of nearby point source emissions. | ||||||||||
| Total Emissions In Each Location Category Within 50 km (1996 tons) | ||||||||||
| Monitor ID | State | County | Monitored Conc. (mg/m3) | Modeled Conc. (mg/m3) |
Underest. Factor | County Defaulted | Zip Code Defaulted | Not Defaulted, Inside County | Not Defaulted, Outside County | |
| 120571066 | Florida | Hillsborough | 0.48 | 0.01 | 83 | 1.54 | 0.00 | 60.36 | 0.00 | |
| 120571067 | Florida | Hillsborough | 0.42 | 0.01 | 63 | 1.54 | 0.00 | 60.36 | 0.00 | |
| 120571071 | Florida | Hillsborough | 1.69 | 0.00 | 691 | 0.00 | 0.00 | 61.33 | 0.00 | |
| 170310068 | Illinois | Cook | 0.33 | 0.01 | 45 | 0.55 | 0.00 | 19.99 | 0.00 | |
| 171191012 | Illinois | Madison | 1.87 | 0.01 | 298 | 0.00 | 0.00 | 2.24 | 0.00 | |
| 171191013 | Illinois | Madison | 1.01 | 0.01 | 167 | 0.00 | 0.00 | 2.24 | 0.00 | |
| 171191015 | Illinois | Madison | 0.80 | 0.01 | 131 | 0.00 | 0.00 | 2.24 | 0.00 | |
| 180350008 | Indiana | Delaware | 0.34 | 0.03 | 11 | 2.16 | 0.24 | 6.02 | 2.74 | |
| 270370462 | Minnesota | Dakota | 0.46 | 0.03 | 17 | 6.66 | 0.00 | 4.80 | 0.00 | |
| 270370463 | Minnesota | Dakota | 0.36 | 0.01 | 27 | 6.66 | 0.00 | 4.80 | 0.00 | |
| 290870006 | Missouri | Holt | 0.56 | 0.00 | 120 | 0.00 | 0.00 | 2.90 | 0.00 | |
| 290870008 | Missouri | Holt | 0.56 | 0.01 | 50 | 0.00 | 0.00 | 2.90 | 0.00 | |
| 290930016 | Missouri | Iron | 0.84 | 0.03 | 33 | 2.64 | 0.00 | 5.07 | 0.00 | |
| 290930020 | Missouri | Iron | 0.35 | 0.02 | 15 | 2.64 | 0.00 | 5.07 | 0.00 | |
| 290930021 | Missouri | Iron | 0.58 | 0.03 | 20 | 2.64 | 0.00 | 5.07 | 0.00 | |
| 300490714 | Montana | Lewis and Clark | 2.21 | 0.14 | 16 | 0.00 | 0.00 | 21.52 | 0.00 | |
| 300490726 | Montana | Lewis and Clark | 1.01 | 0.06 | 18 | 0.00 | 0.00 | 21.52 | 0.00 | |
| 300490727 | Montana | Lewis and Clark | 2.23 | 0.13 | 17 | 0.00 | 0.00 | 21.52 | 0.00 | |
| 310550049 | Nebraska | Douglas | 3.79 | 0.10 | 40 | 0.01 | 0.00 | 21.27 | 0.00 | |
| 420110202 | Pennsylvania | Berks | 0.40 | 0.03 | 13 | 0.06 | 0.00 | 5.64 | 0.00 | |
| 420110203 | Pennsylvania | Berks | 0.55 | 0.03 | 17 | 0.06 | 0.00 | 5.64 | 0.00 | |
| 421010049 | Pennsylvania | Philadelphia | 0.77 | 0.06 | 13 | 0.18 | 0.00 | 1.65 | 0.01 | |
| 421010449 | Pennsylvania | Philadelphia | 3.67 | 0.04 | 104 | 0.18 | 0.00 | 1.65 | 0.01 | |
| 421010549 | Pennsylvania | Philadelphia | 0.38 | 0.04 | 11 | 0.18 | 0.00 | 1.65 | 0.01 | |
| 471570045 | Tennessee | Shelby | 0.99 | 0.04 | 24 | 0.00 | 0.00 | 3.83 | 0.00 | |
| 471870100 | Tennessee | Williamson | 0.57 | 0.02 | 24 | 0.51 | 0.00 | 3.11 | 0.00 | |
| 471870104 | Tennessee | Williamson | 0.34 | 0.02 | 17 | 0.51 | 0.00 | 3.11 | 0.00 | |
| 471871101 | Tennessee | Williamson | 0.62 | 0.01 | 56 | 0.51 | 0.00 | 3.11 | 0.00 | |
| 480850009 | Texas | Collin | 0.42 | 0.03 | 13 | 4.02 | 0.00 | 2.26 | 0.00 | |
| 550090021 | Wisconsin | Brown | 0.48 | 0.00 | 494 | 0.00 | 0.00 | 0.40 | 0.00 | |
|
Some of the monitors do not have significant emissions nearby. The monitors in Madison County, Illinois; Holt County, Missouri; Philadelphia County, Pennsylvania; and Brown County, Wisconsin have less than 3 tons of lead point source emissions within 50 km. This could mean that some lead sources are missing in the NTI in these areas. None of these four states were in the "low participation" category with their point source inventory in section IV.B.ii.a above, however. Some other discordant monitors have a large percentage of emissions nearby falling into one of the three "uncertain" location categories; for example, the monitor in Indiana has several sources which fall more than 5 km outside the reported county (more on Indiana later), and the three monitors in Minnesota and Texas have a large percentage of county-defaulted emissions nearby. For some of the other monitors, we were able to do a "before and after" test. Six of the source-oriented monitors are near three large lead sources which were defaulted in the "penultimate" model run, but located more accurately in the final model run. We can compare the agreement between model and monitors before the sources were located accurately to after. Some other changes to the modeling system were made between the penultimate and final model runs, but we believe the correction of defaulted locations is the most important change affecting the model estimates for these source-oriented lead monitors. 1) The Missouri Source. The source in Missouri (NTI Site ID ES0912) emits 2.90 tons/year of lead and is close to the two discordant monitors in Holt County, Missouri. Defaulted, the source was about 10.6 km from the monitors. The true location of the source is within .7 km of both monitors. There are no other sources nearby. |
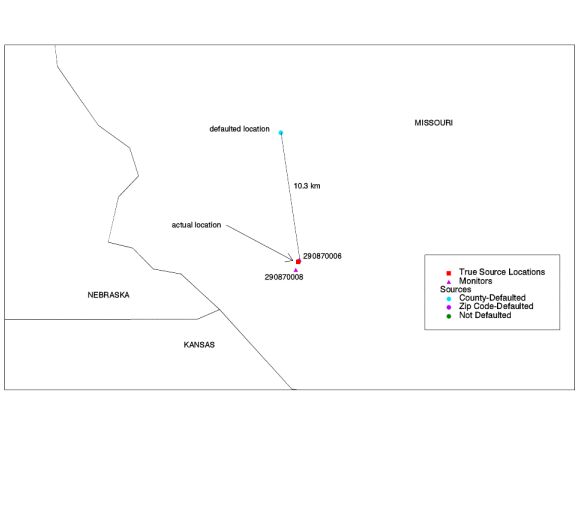 |
| Figure 6. Defaulted lead point source in Missouri. The source is located right next to the monitors, but its location was defaulted to 10 km from the monitors. |
The following table compares the model-to-monitor agreement before to
after.
| Table 12. Model-to-monitor agreement for Holt County lead monitors, before and after source was accurately located. | |||||||
| Defaulted (Before) | Corrected (After) | ||||||
| Monitor ID | State | County | Monitored Conc. (mg/m3) | Modeled Conc.
(mg/m3) |
Underest. Factor | Modeled Conc.
(mg/m3) |
Underest. Factor |
| 290870006 | Missouri | Holt |
0.56 |
0.00 | 311 | 0.00 | 120 |
| 290870008 | Missouri | Holt | 0.56 | 0.00 | 350 | 0.01 | 50 |
|
The model estimates are still much lower than the monitors, but the agreement is improved. 2) The Tennessee Source. The source in Tennessee (NTI Site ID ES099) is in Memphis. It emits 2.70 tons/year of lead and is close to two source-oriented monitors in county 47157 (Shelby County, Tennessee). One monitor is discordant, i.e., underestimation factor of greater than 10, and the other is not. Defaulted, the source was about 13 km from the monitors. Again, the true location is right next to the monitors - within .1 km. The only other large source in the area (3.2 tons/year) is about 10 km away. |
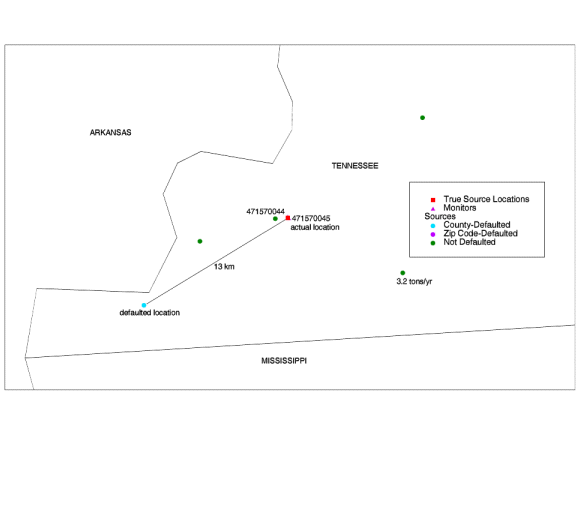 |
| Figure 7. Defaulted lead point source in Tennessee. The source is located right next to the monitors, but its location was defaulted to 13 km from the monitors. The correction improved the model-to-monitor agreement considerably. |
The following table compares the model-to-monitor agreement before to
after for these two monitors.
| Table 13. Before-and-after model-to-monitor agreement for Shelby County lead monitors. | |||||||
| Defaulted (Before) | Corrected (After) | ||||||
| Monitor ID | State | County | Monitored Conc. (mg/m3) | Modeled Conc.
(mg/m3) |
Underest. Factor | Modeled Conc.
(mg/m3) |
Underest. Factor |
| 471570044 | Tennessee | Shelby |
1.80 |
0.01 | 327 | 0.29 | 6 |
| 471570045 | Tennessee | Shelby | 0.99 | 0.01 | 181 | 0.04 | 24 |
Agreement here improves quite a bit, even though the source is not that large.
3) The Florida Source. The source in Florida (NTI Site ID EM3440) is in Tampa. It emits 0.60 tons/year of lead, and is
close to the three discordant monitors in Hillsborough County, Florida. Defaulted, was about 5.9 km from two of the
monitors and 16 km from the third. Its true location is 4.85 from the pair and 6.12 km from the other.
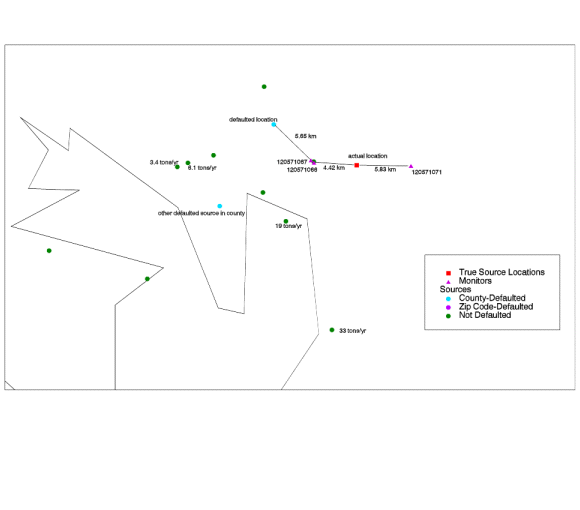 |
| Figure 8. Defaulted lead point source in Florida. The correction did not improve model-to-monitor agreement in this case. It is possible that there is a large point source near the monitors which is missing from or mislocated in the NTI. |
The following table compares the model-to-monitor agreement before to after for these three monitors.
| Table 14. Before-and-after model-to-monitor agreement for Hillsborough County lead monitors. | |||||||
| Defaulted (Before) | Corrected (After) | ||||||
| Monitor ID | State | County | Monitored Conc. (mg/m3) | Modeled
Conc.
(mg/m3) |
Underest. Factor | Modeled
Conc.
(mg/m3) |
Underest. Factor |
| 120571066 | Florida | Hillsborough |
0.48 |
0.01 | 72 | 0.01 | 83 |
| 120571067 | Florida | Hillsborough | 0.42 | 0.01 | 56 | 0.01 | 63 |
| 120571071 | Florida | Hillsborough | 1.69 | 0.00 | 565 | 0.00 | 691 |
Because the source is small and its true location is close to its defaulted location, the model estimates did not change drastically. Yet, these monitors are underestimated drastically by the model. The underestimation factors at all three monitors actually increased slightly. This is in part due to the other changes in the modeling system between the penultimate and final model runs. It is possible that a source is missing or mislocated (in that the source should appear near these monitors--particularly at monitor 120571071 which has an especially severe underestimate). There is another source of similar size (0.50 tons/year) which is also defaulted in this county. Its true location is unknown. There are large sources in the area for which the state reported location had no obvious problems, but these are not reported to be particularly close to the three monitors (about 19 km away). In the first two before-and-after cases, when we located the source correctly, the model estimates were much improved, but still lower than the monitor averages. The best agreement we found was an underestimation by a factor of six, for monitor ID 471570044. This result suggests that, while not the only cause, location defaulting can contribute significantly to underestimation for source-oriented lead monitors. One of the most interesting discordant monitors is 170310068. It is in Chicago, very close to Lake Michigan and the Indiana state line. This site and the surrounding area are shown in the map below. There are six large (>1 ton/year) sources in Indiana which fall within 50 km of this monitor. These are circled in the map. One possible explanation for the underestimate at this site is that these six large Indiana sources are mislocated. In general, many of the Indiana sources have reported locations which place them in Kentucky and Ohio, probably south and east of their true locations. Thus, some of the Indiana sources are offset to the southeast. If the six large Indiana sources in the circle are moved northwest, they will be much closer to the monitor than they are now, which would presumably increase the model estimate at the monitor site. Overall, of the 1333 lead emissions sources identified as belonging to Indiana, 155 (11.6%) have latitude/longitude coordinates that place them outside of Indiana, accounting for 5.7% of the emissions. This would also explain the underestimate at the monitor in Indiana (180350008). Further support for the theory that these six sources are mislocated comes from the surrounding area. There are no big cities near the circled sources. If they are moved northwest, they move into the heavily industrialized cities of Hammond and Gary. |
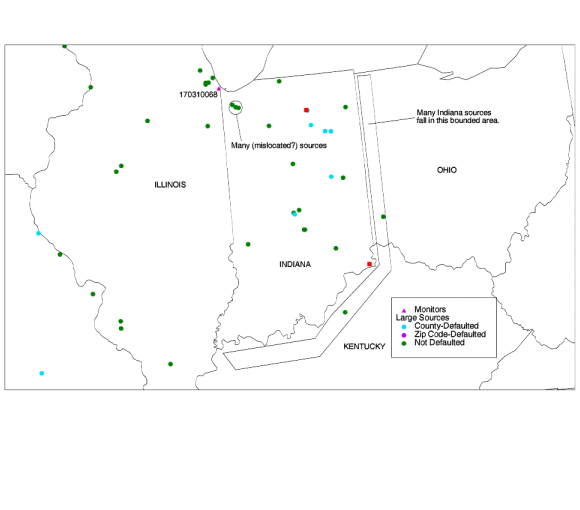 |
| Figure 9. Possible mislocated point sources in Indiana. Some of the Indiana sources are offset to the southeast. We wonder if the sources in the circle are offset to the southeast as well. (Only sources with emissions > 1 ton/year are shown here.) |
In light of these results, it is possible that the current state of the NTI's source location data precludes point-to-point, model-to-monitor comparisons for point source oriented monitors (this is particularly true for metal concentrations which tend to decay rapidly with distance from the source due to their high particle size and weight). It may be that point-to-point, model-to-monitor comparisons for source-oriented monitors should be done only on a small scale, where emissions and source locations can be more accurately characterized. Lead stands out as the most underestimated pollutant in the comparison. This may be due to re-entrainment, the presence of a large number of source oriented monitors, or some other reason. A more detailed investigation needs to be conducted to ascertain why lead is so acutely underestimated pollutant in this model-to-monitor comparison. ii) Cadmium.Of the 20 cadmium monitors, 7 are in the Chicago area, and 6 are spread throughout New York. The 6 New York monitors are all underestimated by a factor of five or greater. Two of the 7 Chicago monitors are estimated within a factor of 2, with the other 5 being underestimated. However, there are higher modeled concentrations within 30 km of all but one of these 13 monitors. Nationwide, 15 of the 20 monitors have higher modeled concentations within 30 km. |
| Table 15. MAXTOMON table for cadmium. For five of the 20 cadmium monitors, no higher modeled concentration can be found within 30 km. | |||||||||
| Percent Missing Low at Radius Of: | |||||||||
| Pollutant | # Monitors | 0 km (Exact Monitor Location) |
2 km | 4 km | 6 km | 8 km | 10 km | 20 km | 30 km |
| Cadmium | 20 | 85% | 85% | 75% | 75% | 75% | 60% | 35% | 25% |
iii) Chromium.Of the 36 chromium monitors, 10 are in Staten Island, NY; 8 are in the Chicago area; and 14 are spread throughout California. The ten monitors in Staten Island are all underestimated by factors of between 6.64 and 8.30. The monitor averages are very similar among the ten sites. There are no census tracts on Staten Island with modeled concentrations similar to the monitors, but there are tracts within 20 km of the monitors with modeled concentrations higher than all 10 monitor averages. However, the eight monitors near Chicago are generally estimated accurately at the monitor locations. The model-to-monitor ratios are all between 0.65 and 1.13, so all are easily estimated within a factor of 2, and all but one are estimated within 30%. The California monitors are estimated inconsistently. Only 2 of the 14 are estimated within a factor of 2 at the exact monitor locations. Of the other 12 montiors studied, 2 are overestimated and 10 are underestimated. These state-to-state differences suggest differences in State inventories. The results for cadmium suggest the possibility that New York has low emissions estimates for cadmium as well. Possible differences in monitoring must also be considered. VI. Conclusions & RecommendationsIn general, at the exact monitor locations, the model estimates were lower than the monitor averages for most of the pollutant/monitor combinations. Only benzene showed good agreement at the exact monitor locations. However, for some of the HAPs, especially lead, it seems likely that the modeling system is systematically underestimating monitored concentrations. By "modeling system", we mean to emphasize that the estimates are the result of: emission estimates We tried to use the MAXTOMON test to see whether the model was mislocating the peak concentrations, or systematically underestimating. On a pollutant-by-pollutant basis, here are the percent of sites underestimated at different radii, out to 50 km: |
In Table 16, each pollutant has an entry that has been marked by an asterisk. This represents the distance away from the monitor where the effect of the uncertainty distance begins to wane. In general, we might say that the modeling system has uncertainty in locating source impacts to within 20 km. But even as we radially reach 50 km, many of the pollutant/monitor combinations are still underestimated for all HAPs except benzene and perchloroethylene. This suggests systematic underestimation of the aldehydes and metals. In general, we think that the most effective way to improve agreement between the model estimates and monitor averages is to improve the emissions inventory. One possibility would be to conduct a study on a small sample of sources in an effort to investigate whether emissions rates are accurately estimated. But if these model estimates are used on a local scale, we think it is crucial
to:
As it stands now, we certainly think it is a mistake to attribute the model estimates to a census tract. The spatial distribution of concentrations within an area of any size is uncertain. Any particular model estimate may be too high or too low, compared with actual conditions that existed in 1996. However, the available data suggest that the model estimate for any particular HAP/location combination is more likely to be lower than actual 1996 conditions, rather than higher.
VII. References2Rosenbaum, A.S., Stiefer, P.S., and Iwamiya, R.K., (1999): Air Toxics Data Archive and AIRS Combined Data Set: Data Base Descriptions. Prepared for US EPA by Systems Applications International, SYSAPP 98/05r. 3Code of Federal Regulations, Title 40, Part 136, Appendix B, Revision 1.11. 4Curran, T.C., and Steigerwald, B.G., (1982): Data Analysis Consequences of Air Quality Measurement Uncertainty. Paper presented at the 75th Annual Meeting of the Air Pollution Control Association, New Orleans, Louisiana, June 1982. 5Meade, P.J., and Pasquill, F., (1958): A study of the average distribution of pollution around Stayhorpe. Int. J. Air Pollution. Pergamon Press. Vol. 1, pp. 60-70. 6Lucas, D.H., (1958): The Atmospheric Pollution of Cities. Int. J. Air Pollution. Pergamon Press. Vol. 1, pp. 71-86. 7Pooler, F., (1961): A prediction model of mean urban pollution for use with standard wind roses. Int. J. Air and Water Pollution. Vol. 4(3/4):199-211. 8Martin, D.O., (1971): An urban diffusion model for estimating long term average values of air quality. J. of the Air Pollution Control Association. Vol 21(1):16-19. 9Calder, K.L., (1971): A climatological model for multiple source urban air pollution. Paper presented at First Meeting of the NATO/CCMS Panel on Modeling. Paper published in Appendix D of User's Guide for the Climatological Dispersion Model. EPA-R4-73-024. Office of Research and Development, U.S. Environmental Protection Agency, Research Triangle Park, NC 27711, pages 73-105. 10Turner, D.B. and Edmisten, N.G., (1968): St. Louis SO2 dispersion model study - description of basic data. (Unpublished report, Division of Meteorology, NAPCA). Atmospheric Sciences Modeling Division, U.S. Environmental Protection Agency, Research Triangle Park, NC 27711. 11Turner, D.B., Zimmerman, J.R., and Busse, A.D., (1971): An evaluation of some climatological models. Paper presented at Third Meeting of the NATO/CCMS Panel on Modeling. Paper published in Appendix E of User's Guide for the Climatological Dispersion Model. EPA-R4-73-024. Office of Research and Development, U.S. Environmental Protection Agency, Research Triangle Park, NC 27711, pages 107-131. 12Briggs, G.A., (1969): Plume Rise. TID-25075. U.S. Atomic Energy Commission, Available from the National Technical Information Service, U.S. Department of commerce, Springfield, VA 22151, 85 pages. 13Holland, J.A., (1953): A meteorological survey of the Oak Ridge area: final report covering the period 1948-1952. U.S. AEC Report ORO-99. Technical Information Service, Weather Bureau, Oak Ridge, TN. pages 554-559. 14Irwin, J.S. and Brown, T.M., (1985): A sensitivity analysis of the treatment of area sources by the Climatological Dispersion Model. J. of the Air Pollution Control Association. Vol 35(4):39-364. 15McElroy, J.L. and Pooler, F., (1968): St. Louis Dispersion Study Volume II-Analysis. National Air Pollution Control Administration. Publication Number AP-53. U.S. Department of Health Education and Welfare, Arlington, VA, 51 pages. 16Gifford, F.S., (1976): Turbulent diffusion-typing schemes: a review. Nuclear Safety. Vol 17(1):68-86. 17Turner, D.B. and Novak, J.H., (1978): User's Guide for RAM, Volume 1, Algorithm Description and Use. EPA-600/8-78-016a. Office of Research and Development, U.S. Environmental Protection Agency, Research Triangle Park, NC 27711, 70 pages. 18U.S. EPA, (1995): User's Guide for the Industrial Source Complex (ISC3) Dispersion Models, Volume I - User Instructions. EPA-454/B-95-003a. Office of Air Quality Planning and Standards, U.S. Environmental Protection Agency, Research Triangle Park, NC 27711, 320 pages. 19Turner, D.B. and Irwin, J.S., (1983): Comparison of sulfur dioxide estimates from the model RAM with St. Louis measurements. Air Pollution Modeling and Its Application II, (Edited by C. De Wispelaere), Plenum Press, pages 695-707. 20Gifford, F.A. and Hanna, S.R., (1973): Modeling urban air pollution. Atmospheric Environment. (7):131-136. 21Hanna, S.A., Briggs, G.A., and Hosker, R.P., (1982): Handbook on Atmospheric Diffusion. Available as DE82002045 (DOE/TIC-11223) from the National Technical Information Service, U.S. Department of Commerce, Springfield, VA, 22161, 108 pages. 22U.S. EPA, (1999): A simplified approach for estimating secondary production of hazardous air pollutants (HAPS) using the OZIPR model. EPA-454R-99-054. U.S. Environment Protection Agency, Research Triangle Park, NC 27711, 86 pages. |
![[logo] US EPA](../gif/logo_epaseal.gif)